Dans ce quiz, les questions sont liées les unes aux autres.
Pensez à bien noter sur une feuille vos réponses au fur et à mesure.
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2
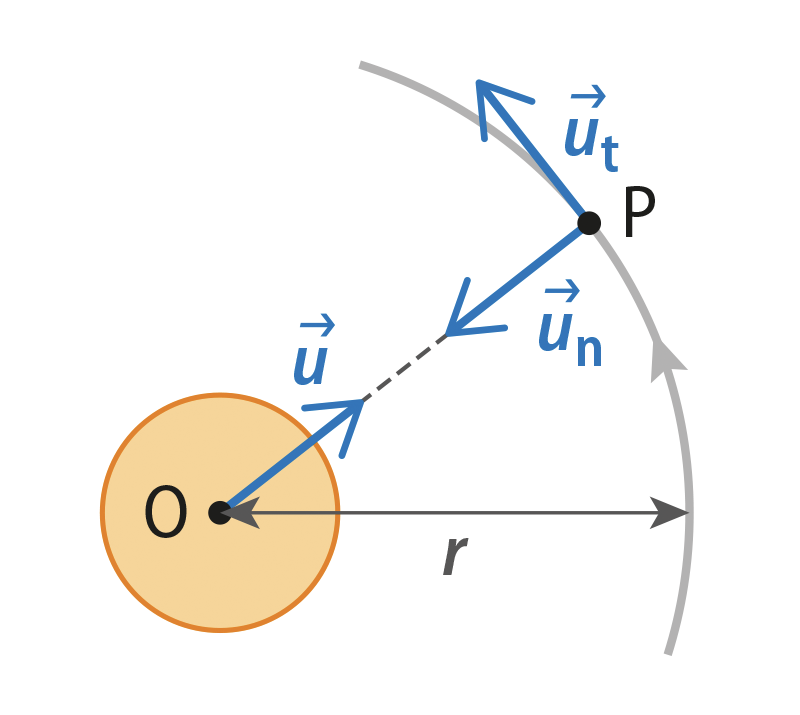
La force gravitationnelle exercée par l’astre sur le satellite est :
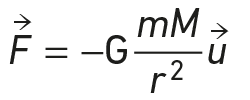
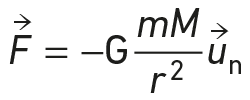
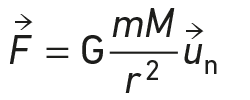
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

L’accélération du satellite est :
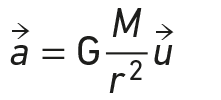
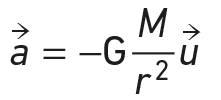
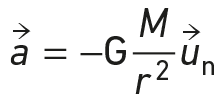
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

On note 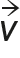 la vitesse du satellite.
Le vecteur accélération
la vitesse du satellite.
Le vecteur accélération 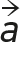 s’écrit aussi :
s’écrit aussi :
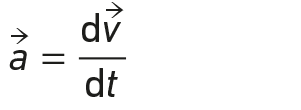
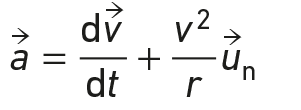
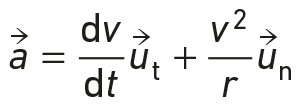
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

Le mouvement d’un tel satellite est uniforme car :
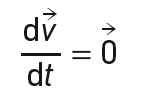
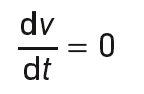
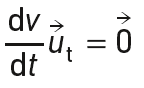
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

Les deux expressions du vecteur accélération 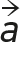 conduisent à l’égalité :
conduisent à l’égalité :
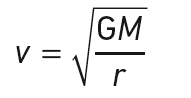
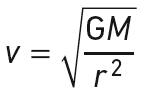
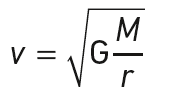
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

Pour r = 778 millions de km, la norme de la vitesse du satellite vaut :
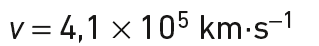

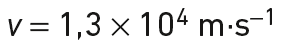
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

La période de révolution de ce satellite est :
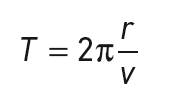
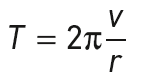
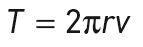
On considère un satellite P de masse m en mouvement circulaire de rayon r autour du centre O d’un astre de masse M = 2,0 × 1030 kg.
Le schéma ci-contre définit les vecteurs unitaires.
L’étude est faite dans le référentiel astrocentrique, supposé galiléen.
Donnée : G = 6,67 × 10-11 N·m2·kg-2

La période de révolution de ce satellite vaut :
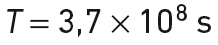
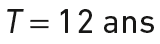
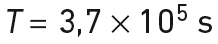
Les demi-grands axes de leurs orbites sont a1 et a2, leurs périodes de révolution sont T1 et T2.
La troisième loi de Kepler permet d’écrire :
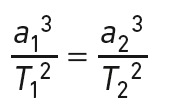
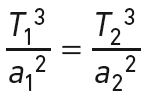
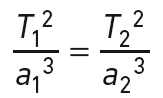
Les demi-grands axes de leurs orbites sont a1 et a2, leurs périodes de révolution sont T1 et T2.
Si T1 = 15 h, a1 = 3,1 × 104 km et T2 = 43 200 s, alors le demi-grand axe a2 du deuxième satellite vaut :
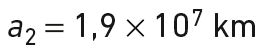
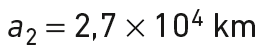
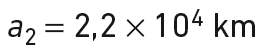
D’après la deuxième loi de Kepler, la vitesse d’un satellite :
est maximale au périastre.
est maximale à l’apoastre.
augmente à l’approche de l’astre.
Un satellite géostationnaire est fixe dans le référentiel :
héliocentrique.
géocentrique.
terrestre.
Laquelle de ces trajectoires circulaires ne vérifie pas la première loi de Kepler ?
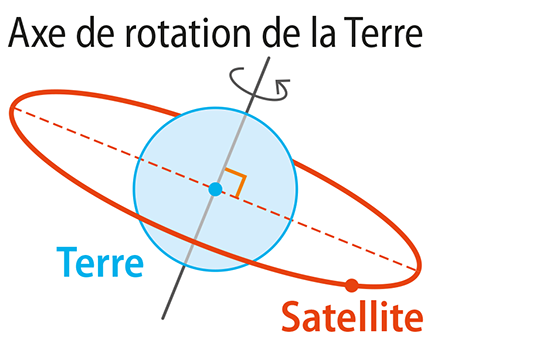
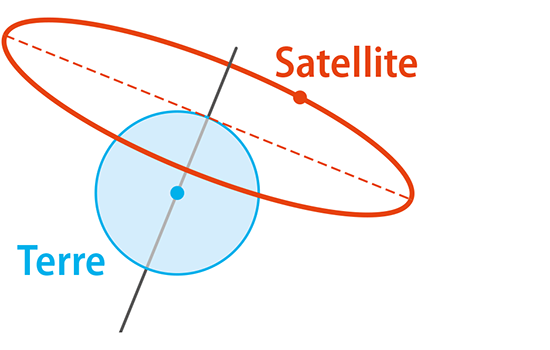
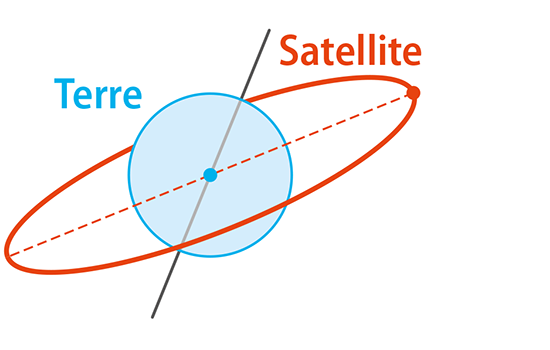
Lequel de ces satellites peut être géostationnaire ?



 QCM
QCM