QCMPour décrire un mouvement, il faut choisir :
un système.
le référentiel terrestre quel que soit le système étudié.
un référentiel.
Pour réviser cette notion, voir la fiche 5 Mouvement d’un système.
Un vecteur vitesse est caractérisé par :
une direction, un sens et une échelle.
une direction, un sens et une valeur.
une direction, un sens et une norme.
Pour réviser cette notion, voir la fiche 5 Mouvement d’un système.
La valeur vi de la vitesse d’un point M entre deux positions Mi et Mi+1 successives séparées par une durée ∆t est telle que :
Pour réviser cette notion, voir la fiche 5 Mouvement d’un système.
Dans un référentiel donné, si un point modélisant un système a un mouvement rectiligne uniforme alors au cours du mouvement son vecteur vitesse :
est égal au vecteur nul.
ne varie pas.
varie.
Pour réviser cette notion, voir la fiche 5 Mouvement d’un système.
Les vecteurs vitesse d’un point A modélisant un système sont représentés ci-dessous.
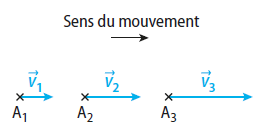
Le mouvement est rectiligne uniforme.
Le mouvement est rectiligne décéléré.
Le mouvement est rectiligne accéléré.
Pour réviser cette notion, voir la fiche 5 Mouvement d’un système.
Une action est modélisée par :
un vecteur.
un système.
une force.
Pour réviser cette notion, voir la fiche 6 Modélisation d’une action par une force.
Une force est représentée par :
un segment.
un vecteur.
une double flèche.
Pour réviser cette notion, voir la fiche 6 Modélisation d’une action par une force.
Les forces s’exerçant sur un système modélisé par un point G sont représentées ci-dessous.
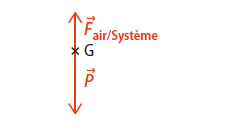
Ces deux forces ont :
la même direction.
le même sens.
des sens contraires.
Pour réviser cette notion, voir la fiche 6 Modélisation d’une action par une force.
La valeur
Pour réviser cette notion, voir la fiche 6 Modélisation d’une action par une force.
Pour calculer la valeur
les masses mA et mB en grammes et la distance
les masses mA et mB en kilogrammes et la distance
les masses mA et mB en kilogrammes et la distance
Pour réviser cette notion, voir la fiche 6 Modélisation d’une action par une force.
Les forces d’interaction gravitationnelle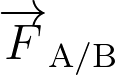 
et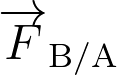 
s’exerçant entre deux systèmes A et B sont représentées par le schéma :
Pour réviser cette notion, voir la fiche 6 Modélisation d’une action par une force.
Si un système est en mouvement rectiligne uniforme alors :
une seule force s’exerce sur le système.
aucune force ne s’exerce sur le système.
la somme vectorielle des forces qui s’exercent sur le système est nulle.
Pour réviser cette notion, voir la fiche 7 Lois de Newton.
Si les forces exercées sur un système se compensent alors :
le système peut être immobile.
le système peut être en mouvement rectiligne accéléré.
le système peut être en mouvement rectiligne uniforme.
Pour réviser cette notion, voir la fiche 7 Lois de Newton.
Si la somme vectorielle des forces exercées sur un système n’est pas nulle alors :
le mouvement du système n’est pas rectiligne uniforme.
le système n’est pas immobile.
le mouvement du système est rectiligne uniforme.
Pour réviser cette notion, voir la fiche 7 Lois de Newton.
Si un système A exerce une force sur un système B, alors le système B exerce sur le système A une force :
de même direction, de même valeur et de même sens.
de même direction, de même valeur et de sens contraire.
de direction contraire, de même valeur et de même sens.
Pour réviser cette notion, voir la fiche 7 Lois de Newton.