Le rapport des valeurs des forces d’interaction électrostatique et gravitationnelle s’exerçant entre un anion et un cation au sein d’un solide ionique est égal à 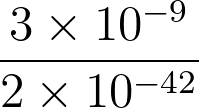 soit :
soit :
1,5 × 10–51
1,5 × 10–33
1,5 × 1033
Fiche 32 Manipuler les puissances de 10
La concentration en quantité de matière d’un soluté dissous en solution est égale à 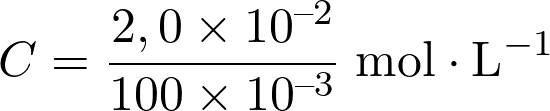 soit :
soit :
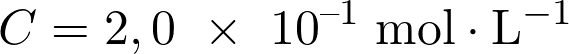
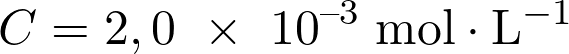
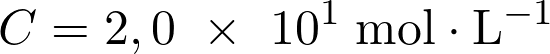
Fiche 32 Manipuler les puissances de 10
Le rayon de la Terre est
Fiche 32 Manipuler les puissances de 10
La longueur d’onde d’une onde ultrasonore est 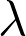 = 0,80 cm soit :
= 0,80 cm soit :
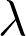 = 8,0 × 10–3 m
= 8,0 × 10–3 m
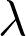 = 8,0 × 10–4 m
= 8,0 × 10–4 m
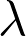 = 8,0 × 10–1 m
= 8,0 × 10–1 m
Fiche 32 Manipuler les puissances de 10
La fréquence limitant les domaines des ultraviolets du visible est
Fiche 32 Manipuler les puissances de 10
L’ordre de grandeur de la constante de Planck h = 6,62 × 10–34 J·s est :
10 –34 J·s
10 –35 J·s
10 –33 J·s
Fiche 32 Manipuler les puissances de 10
La masse d’un atome d’argent est 1,82 × 10–25 kg ; celle d’un nucléon 1,67 × 10–27 kg. Le nombre de nucléons dans le noyau de cet atome est :
109
9
10
Fiche 33 Utiliser la proportionnalité
La valeur de la force d’interaction gravitationnelle s’exerçant entre deux corps de masse 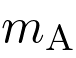 et
et 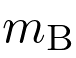 distants de
distants de 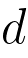 est :
est :
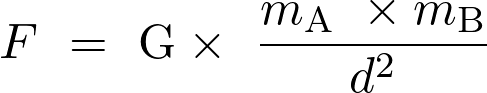 .
.
Si la masse 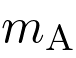 est multipliée par 2, la valeur de la force d’interaction gravitationnelle est :
est multipliée par 2, la valeur de la force d’interaction gravitationnelle est :
multipliée par 4.
multipliée par 2.
divisée par 2.
Fiche 33 Utiliser la proportionnalité
D’après la loi de Mariotte,  = constante. La représentation graphique modélisant cette situation de proportionnalité est :
= constante. La représentation graphique modélisant cette situation de proportionnalité est :
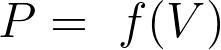
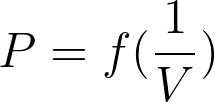
Fiche 33 Utiliser la proportionnalité
Le rendement d’une synthèse est égal à 60 % soit :


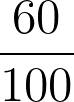
Fiche 33 Utiliser la proportionnalité
La quantité de matière d’un gaz et son volume sont liés par la relation 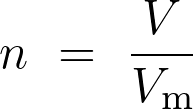 .
.
Le volume molaire du gaz est :
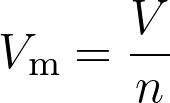
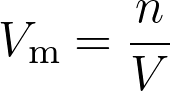
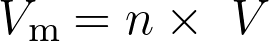
Fiche 34 Manipuler une expression littérale
La relation à l’équivalence d’un titrage s’écrit : 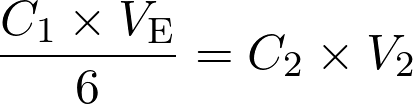 .
.
Le volume à l’équivalence 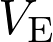 est :
est :
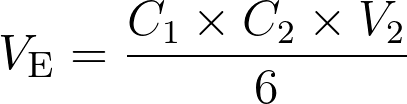
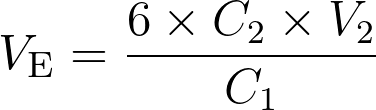
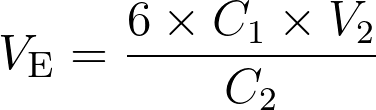
Fiche 34 Manipuler une expression littérale
L’avancement maximal d’une transformation chimique est tel que 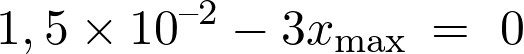 soit :
soit :
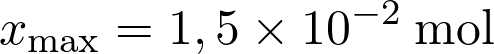
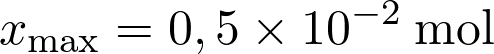
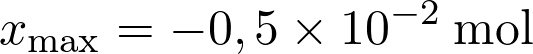
Fiche 35 Résoudre une équation
L’intensité du courant dans un circuit est telle que 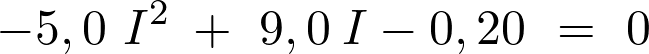
soit :
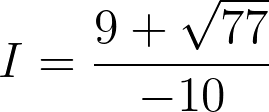
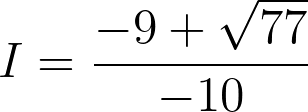
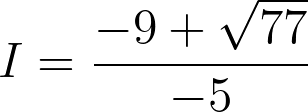
Fiche 35 Résoudre une équation
La distance
L’équation admet deux solutions.
La seule solution acceptable en physique est
La seule solution acceptable en physique est
Fiche 35 Résoudre une équation
On repère la position M d’un pendule de longueur
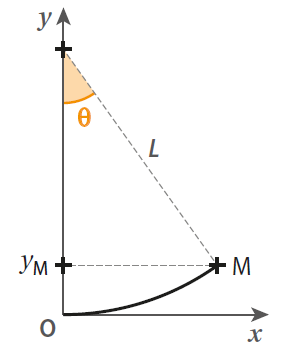
Fiche 36 Utiliser les relations dans un triangle
Une lentille mince convergente donne d’un objet plan AB une image réelle A’B’ comme schématisé ci-dessous.
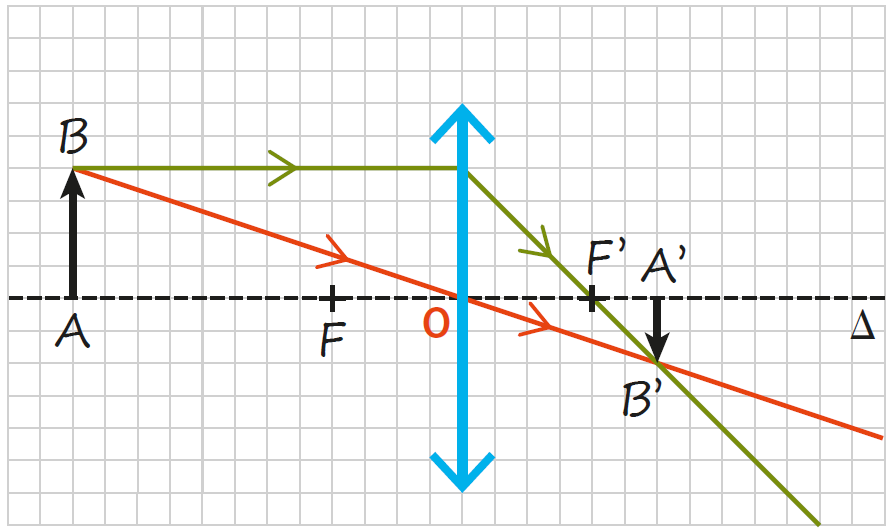
Le rapport de la taille de l’image et de celle de l’objet vérifie la relation :
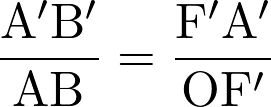
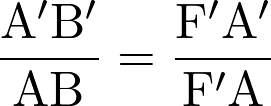
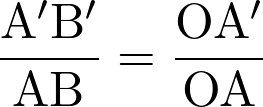
Fiche 36 Utiliser les relations dans un triangle
Le graphique représentant l’évolution de la vitesse d’un système en fonction du temps est donné ci-dessous.
L’équation de la droite de modélisation est :
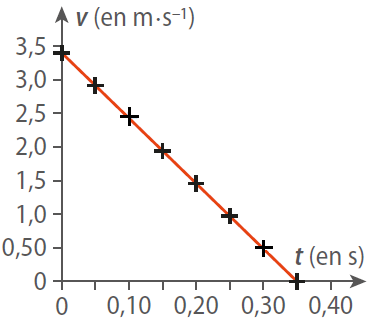
Fiche 38 Déterminer l’équation d’une droite
Une modélisation par régression linéaire d’une série de mesures est donnée ci-dessous.
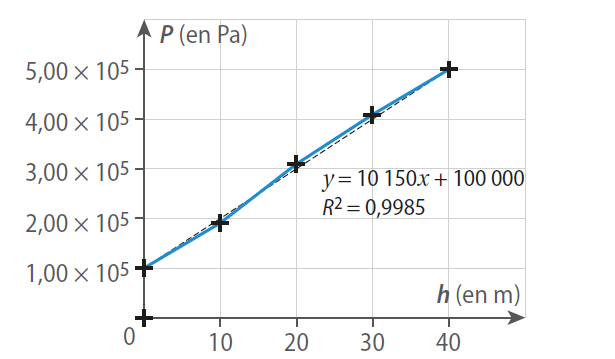
Le coefficient de détermination est différent de 1, la modélisation est incorrecte.
L’équation de la droite de régression est
L’équation de la droite de régression est
Fiche 39 Exploiter une modélisation par régression linéaire
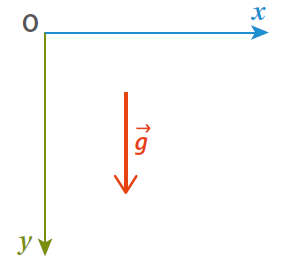
Les coordonnées du vecteur champ de pesanteur 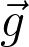 sont :
sont :
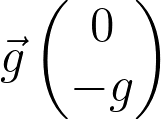
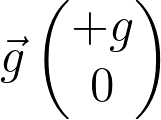
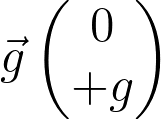
Fiche 41 Utiliser les vecteurs
Les forces s’exerçant sur un pendule sont représentées ci-dessous.
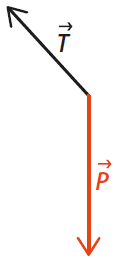
La somme vectorielle de ces forces est :
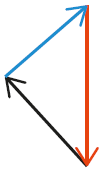
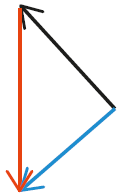
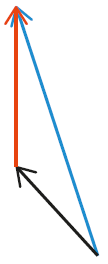
Fiche 42 Sommer et soustraire des vecteurs
Les vecteurs vitesse d’un système sont représentés ci-dessous.
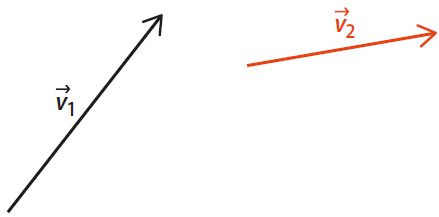
Le vecteur 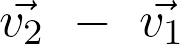 est :
est :
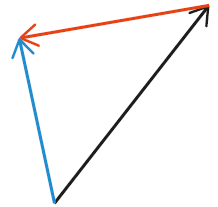
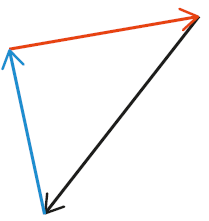
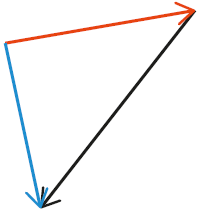
Fiche 42 Sommer et soustraire des vecteurs
Le produit scalaire 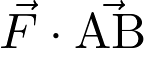 est égal à :
est égal à :
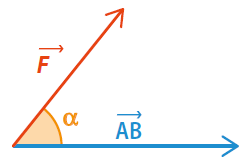
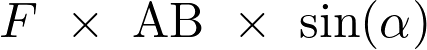
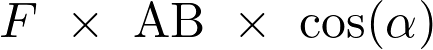
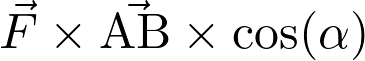
Fiche 43 Calculer un produit scalaire
Le travail d’une force se déplaçant de A vers B est égal au produit scalaire 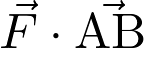 . Le travail est maximal si :
. Le travail est maximal si :
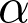 = 90°
= 90°
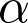 = 180°
= 180°
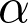 = 0°
= 0°
Fiche 43 Calculer un produit scalaire
Le travail du poids 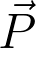 se déplaçant de A vers B est égal :
se déplaçant de A vers B est égal :
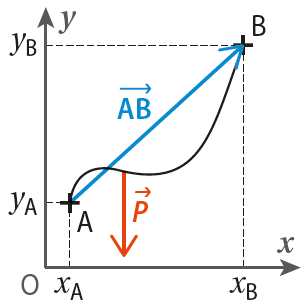
Fiche 43 Calculer un produit scalaire
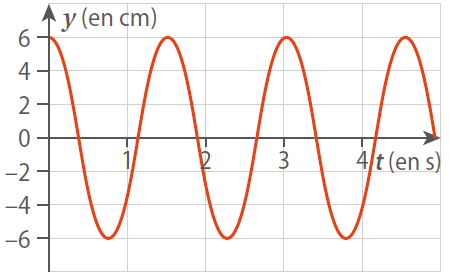
L’élongation 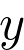 en fonction du temps est représentée par une fonction sinusoïdale d’amplitude
en fonction du temps est représentée par une fonction sinusoïdale d’amplitude
Fiche 45 Utiliser une fonction

L’élongation 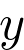 en fonction du temps est représentée par une fonction sinusoïdale de la forme :
en fonction du temps est représentée par une fonction sinusoïdale de la forme :
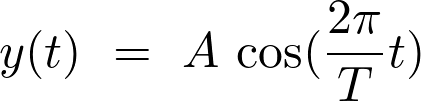
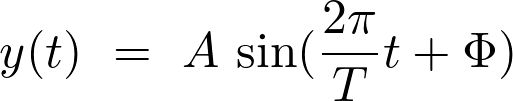
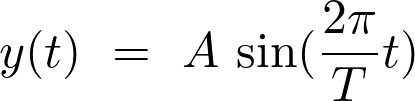
Fiche 45 Utiliser une fonction
 QCM
QCM