QCMLe quotient d’une réaction est égal à
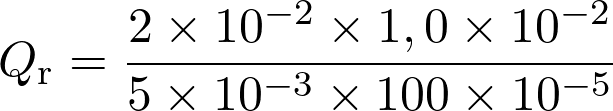
soit :
4 × 10–15
4 × 101
4 × 103
Fiche 32 Manipuler les puissances de 10
La capacité d’un condensateur est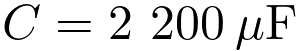 
soit :
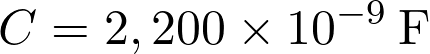
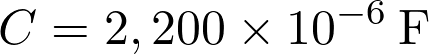
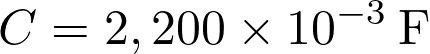
Fiche 32 Manipuler les puissances de 10
L’ordre de grandeur de la charge élémentaire e = 1,60 × 10–19 C est :
10–18 C
10–19
10–19 C
Fiche 32 Manipuler les puissances de 10
La différence de marche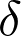 
est proportionnelle à la position 
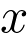d’un point M sur l’écran.
La représentation graphique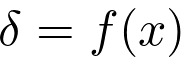 
correcte est :
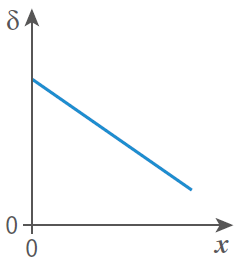
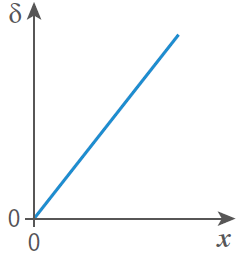
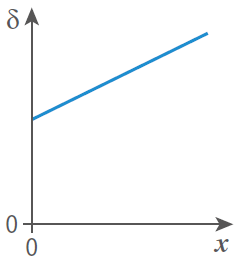
Fiche 33 Utiliser la proportionnalité
Lors de la charge d’un condensateur par une source idéale de tension
0,63 V
6,3 V
3,7 V
Fiche 33 Utiliser la proportionnalité
La charge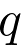 
d’un condensateur et la tension 
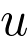à ses bornes sont liées par la relation 
.
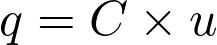La capacité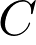 
du condensateur est :
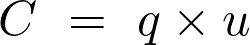
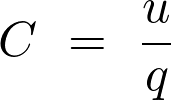
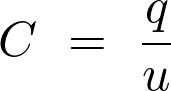
Fiche 34 Manipuler une expression littérale
Le flux thermique 
et la variation de température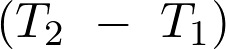 
sont liés par la relation 
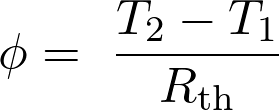. La température 
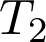est égale à :
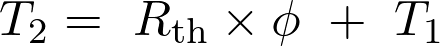
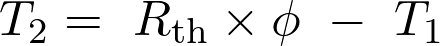
Fiche 34 Manipuler une expression littérale
La 3e loi de Kepler s’écrit :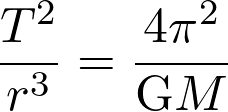 
. La période de révolution 
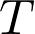est :
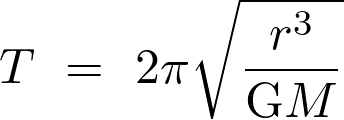
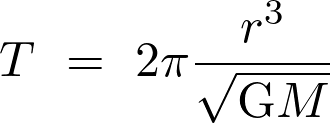
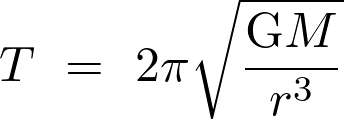
Fiche 34 Manipuler une expression littérale
Pour tracer le graphique
les points sont reliés à la règle si
Fiche 37 Tracer un graphique
Soit le graphique tracé ci-dessous :
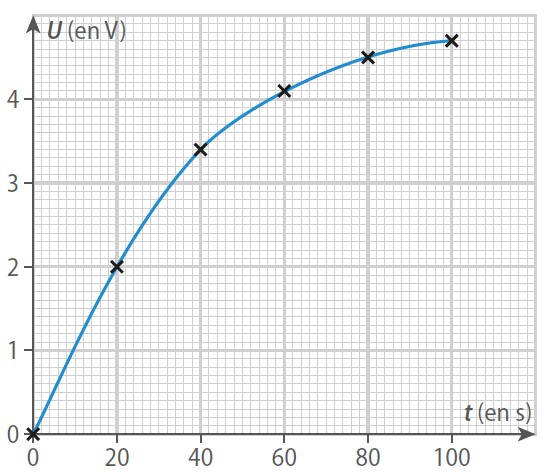
Son titre est
Son titre est
Les points sont correctement représentés.
Fiche 37 Tracer un graphique
Le graphique représentant l’évolution de la différence de marche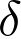 
en fonction de la position
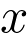d’un point M sur un écran est donné ci-dessous.
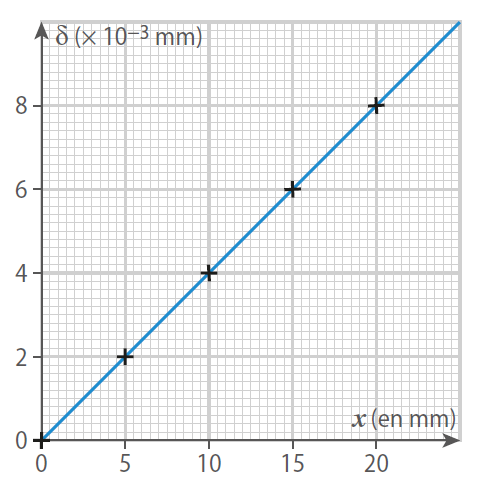
Le coefficient directeur de la droite est :
4 × 10–4
0,4
4 × 10–4 mm2
Fiche 38 Déterminer l’équation d’une droite
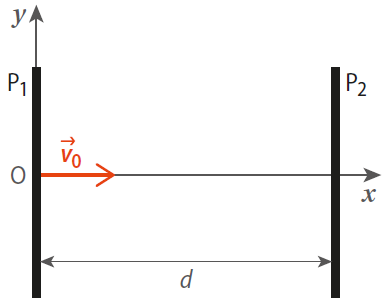
Les coordonnées du vecteur vitesse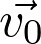 
sont :
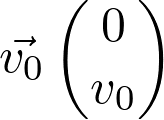
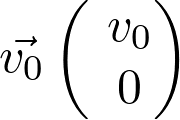
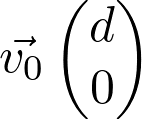
Fiche 41 Utiliser les vecteurs
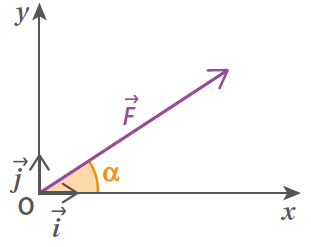
Les coordonnées de la force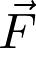 
sont :
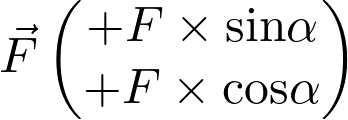
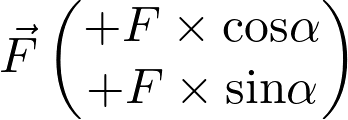
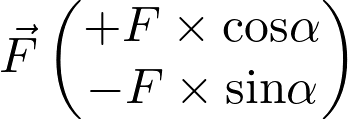
Fiche 41 Utiliser les vecteurs
Les forces s’exerçant sur un système sont représentées ci-dessous.
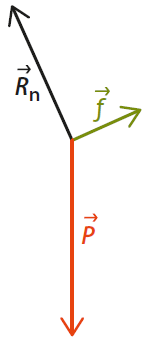
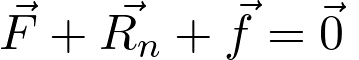
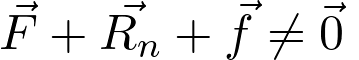
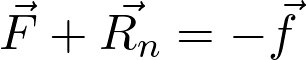
Fiche 42 Sommer et soustraire des vecteurs
Pour une réaction dont la vitesse suit une loi d’ordre 1,
on a :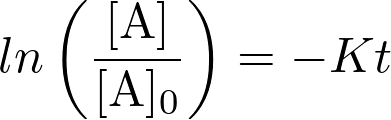 
avec [A] et [A]0 les concentrations en réactifs respectivement à l’instant
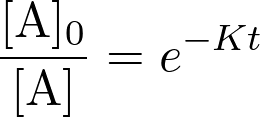
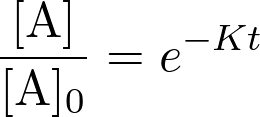
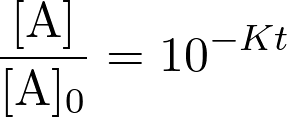
Fiche 45 Utiliser une fonction
La tension aux bornes d’un condensateur lors de sa décharge est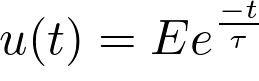 
.
À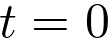 
, 
.
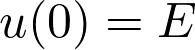Pour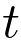 
tendant vers +∞, 
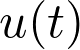tend vers +∞.
Pour 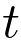tendant vers +∞, 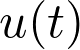tend vers 0.
Fiche 45 Utiliser une fonction
Pour un couple acide faible/base faible, le rapport de la concentration en base par celle en acide est tel que
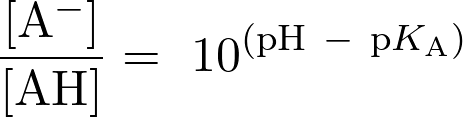soit :
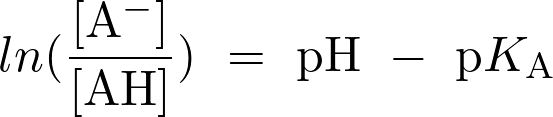
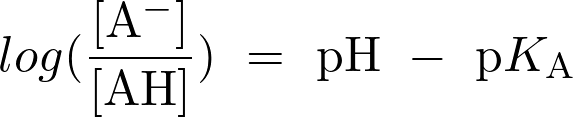
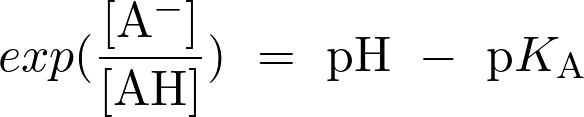
Fiche 45 Utiliser une fonction
Un système pour lequel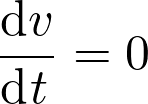 
a un mouvement :
uniformément accéléré.
uniforme.
uniformément ralenti.
Fiche 46 Déterminer la dérivée ou une primitive d’une fonction
On donne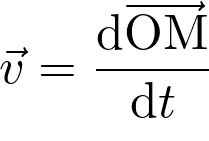 
.
Les coordonnées du vecteur vitesse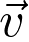 
sont les dérivées des coordonnées du vecteur position 
.
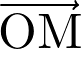Les coordonnées du vecteur vitesse 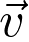sont les primitives des coordonnées du vecteur position .
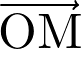Les coordonnées du vecteur position 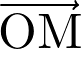sont les primitives des coordonnées du vecteur vitesse .
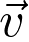Fiche 46 Déterminer la dérivée ou une primitive d’une fonction
On donne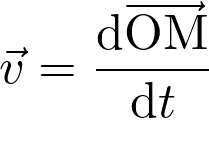 
.
La coordonnée horizontale du vecteur position d’un système est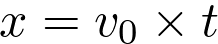 
.
La coordonnée horizontale du vecteur vitesse est :
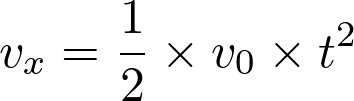
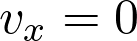
Fiche 46 Déterminer la dérivée ou une primitive d’une fonction
Pour un mouvement rectiligne uniformément accéléré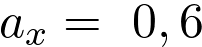 
.
La coordonnée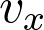 
du vecteur vitesse est telle que 
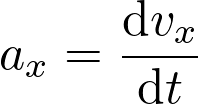soit :
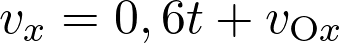
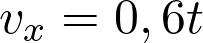
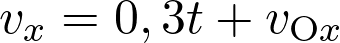
Fiche 46 Déterminer la dérivée ou une primitive d’une fonction
On donne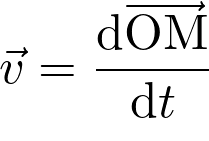 
.
Si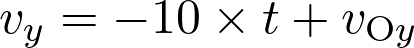 
alors :
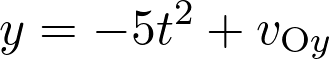
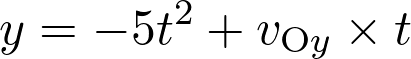
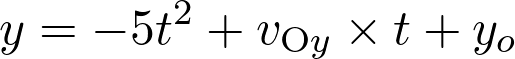
Fiche 46 Déterminer la dérivée ou une primitive d’une fonction
Le coefficient directeur de la tangente à la courbe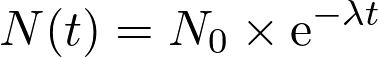 
est :
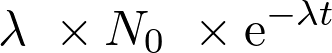
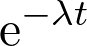
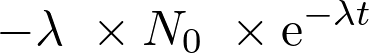
Fiche 46 Déterminer la dérivée ou une primitive d’une fonction
L’équation différentielle dont la solution est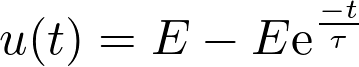 
est de la forme :
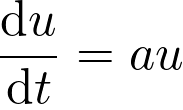avec 
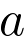une constante non nulle.
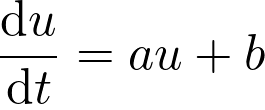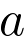avec et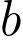 
des constantes et 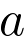non nulle.
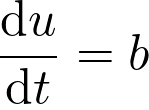avec 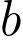une constante.
Fiche 47 Résoudre une équation différentielle
La solution de l’équation différentielle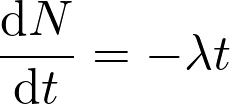 
est :
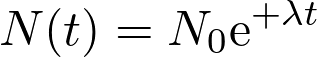
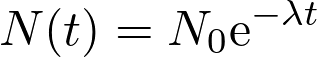
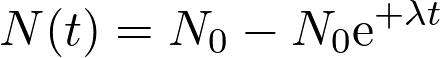
Fiche 47 Résoudre une équation différentielle